Single sample intracellular signalling network inference#
In this notebook we showcase how to use the advanced CARNIVAL implementation available in CORNETO. This implementation extends the capabilities of the original CARNIVAL method by enabling advanced modelling and injection of knowledge for hypothesis generation. We will use a dataset consisting of 6 samples of hepatic stellate cells (HSC) where three of them were activated by the cytokine Transforming growth factor (TGF-β).
We will show how to estimate Transcription Factor activities from gene expression data, following the Decoupler tutorial for functional analysis. Then, we will use RIDDEN to estimate, in a similar fashion, receptor activities. Finally, we will use the CARNIVAL method available in CORNETO to infer a network from receptors to TFs, assuming that we don’t really know which treatment was used.
Please keep in mind that CARNIVAL, as any other method, is designed to facilitate systematic exploration of intracellular signalling hypotheses by leveraging curated knowledge-base networks. It is not intended to produce a single, definitive solution.
Parameter Sensitivity
Alterations in solver settings, threshold values, or choice of prior-knowledge networks can materially affect the inferred network.Data Dependence
The characteristics of your dataset—experimental design, sample size, preprocessing, and normalization—will directly influence model outputs.Knowledge-Base Limitations
Underlying pathway repositories may exhibit incomplete coverage and annotation biases.
Each network generated by CARNIVAL should be regarded as a potential, simplified hypothesis of the real signalling. Users are encouraged to compare multiple configurations and to validate the most promising models through further analysis and experimental validation.
NOTE: This tutorial uses the new Decoupler v2 version. We also use the highs free, open source solver, which has to be installed with
pip install highspy
import gzip
import os
import shutil
import tempfile
import urllib.request
import pandas as pd
# https://decoupler-py.readthedocs.io
import decoupler as dc
import numpy as np
# https://omnipathdb.org/
import omnipath as op
# Pydeseq for differential expression analysis
from pydeseq2.dds import DefaultInference, DeseqDataSet
from pydeseq2.ds import DeseqStats
# https://corneto.org
import corneto as cn
dc.__version__
'2.0.6'
max_time = 300
seed = 0
# Load the dataset
adata = dc.ds.hsctgfb()
adata
AnnData object with n_obs × n_vars = 6 × 58674
obs: 'condition', 'sample_id'
Data preprocessing#
We will use AnnData and PyDeseq2 to pre-process the data and compute differential expression between control and tretament
# Obtain genes that pass the thresholds
dc.pp.filter_by_expr(
adata=adata,
group="condition",
min_count=10,
min_total_count=15,
large_n=10,
min_prop=0.7,
)
adata
AnnData object with n_obs × n_vars = 6 × 19510
obs: 'condition', 'sample_id'
# Build DESeq2 object
inference = DefaultInference(n_cpus=8)
dds = DeseqDataSet(
adata=adata,
design_factors="condition",
refit_cooks=True,
inference=inference,
)
# Compute LFCs
dds.deseq2()
# Extract contrast between conditions
stat_res = DeseqStats(dds, contrast=["condition", "treatment", "control"], inference=inference)
# Compute Wald test
stat_res.summary()
Using None as control genes, passed at DeseqDataSet initialization
Log2 fold change & Wald test p-value: condition treatment vs control
baseMean log2FoldChange lfcSE stat \
RP11-347I19.8 88.877997 -0.207125 0.252557 -0.820110
TMEM170B 103.807801 -0.276960 0.210575 -1.315260
RP11-91P24.6 185.514929 -0.305848 0.180937 -1.690352
SLC33A1 2559.269047 0.595912 0.085253 6.989890
SNORA61 66.168502 0.746770 0.266470 2.802454
... ... ... ... ...
RP11-75I2.3 771.828248 3.812419 0.128113 29.758231
SLC25A24 3525.523888 0.651017 0.087599 7.431750
BTN2A2 674.018191 -0.107905 0.106223 -1.015833
RP11-101E3.5 194.084339 0.092515 0.181973 0.508402
RP11-91I8.3 10.761886 -3.804532 0.920191 -4.134502
pvalue padj
RP11-347I19.8 4.121536e-01 5.540987e-01
TMEM170B 1.884227e-01 3.054162e-01
RP11-91P24.6 9.096068e-02 1.682470e-01
SLC33A1 2.751015e-12 2.426415e-11
SNORA61 5.071542e-03 1.382504e-02
... ... ...
RP11-75I2.3 1.357073e-194 4.487540e-192
SLC25A24 1.071704e-13 1.050701e-12
BTN2A2 3.097088e-01 4.492492e-01
RP11-101E3.5 6.111714e-01 7.290708e-01
RP11-91I8.3 3.557244e-05 1.474126e-04
[19510 rows x 6 columns]
results_df = stat_res.results_df
results_df
| baseMean | log2FoldChange | lfcSE | stat | pvalue | padj | |
|---|---|---|---|---|---|---|
| RP11-347I19.8 | 88.877997 | -0.207125 | 0.252557 | -0.820110 | 4.121536e-01 | 5.540987e-01 |
| TMEM170B | 103.807801 | -0.276960 | 0.210575 | -1.315260 | 1.884227e-01 | 3.054162e-01 |
| RP11-91P24.6 | 185.514929 | -0.305848 | 0.180937 | -1.690352 | 9.096068e-02 | 1.682470e-01 |
| SLC33A1 | 2559.269047 | 0.595912 | 0.085253 | 6.989890 | 2.751015e-12 | 2.426415e-11 |
| SNORA61 | 66.168502 | 0.746770 | 0.266470 | 2.802454 | 5.071542e-03 | 1.382504e-02 |
| ... | ... | ... | ... | ... | ... | ... |
| RP11-75I2.3 | 771.828248 | 3.812419 | 0.128113 | 29.758231 | 1.357073e-194 | 4.487540e-192 |
| SLC25A24 | 3525.523888 | 0.651017 | 0.087599 | 7.431750 | 1.071704e-13 | 1.050701e-12 |
| BTN2A2 | 674.018191 | -0.107905 | 0.106223 | -1.015833 | 3.097088e-01 | 4.492492e-01 |
| RP11-101E3.5 | 194.084339 | 0.092515 | 0.181973 | 0.508402 | 6.111714e-01 | 7.290708e-01 |
| RP11-91I8.3 | 10.761886 | -3.804532 | 0.920191 | -4.134502 | 3.557244e-05 | 1.474126e-04 |
19510 rows × 6 columns
data = results_df[["stat"]].T.rename(index={"stat": "treatment.vs.control"})
data
| RP11-347I19.8 | TMEM170B | RP11-91P24.6 | SLC33A1 | SNORA61 | THAP9-AS1 | LIX1L | TTC8 | WBSCR22 | LPHN2 | ... | STARD4-AS1 | ZNF845 | NIPSNAP3B | ARL6IP5 | MATN1-AS1 | RP11-75I2.3 | SLC25A24 | BTN2A2 | RP11-101E3.5 | RP11-91I8.3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| treatment.vs.control | -0.82011 | -1.31526 | -1.690352 | 6.98989 | 2.802454 | 1.531175 | 2.164055 | -0.579835 | -0.945628 | -14.351065 | ... | 14.484178 | 0.567176 | -1.882852 | -8.425175 | -1.739571 | 29.758231 | 7.43175 | -1.015833 | 0.508402 | -4.134502 |
1 rows × 19510 columns
Estimation of Transcription Factor activities with Deocupler and CollecTRI#
# Retrieve CollecTRI gene regulatory network (through Omnipath).
# These are regulons that we will use for enrichment tests
# to infer TF activities
collectri = dc.op.collectri(organism="human")
collectri
| source | target | weight | resources | references | sign_decision | |
|---|---|---|---|---|---|---|
| 0 | MYC | TERT | 1.0 | DoRothEA-A;ExTRI;HTRI;NTNU.Curated;Pavlidis202... | 10022128;10491298;10606235;10637317;10723141;1... | PMID |
| 1 | SPI1 | BGLAP | 1.0 | ExTRI | 10022617 | default activation |
| 2 | SMAD3 | JUN | 1.0 | ExTRI;NTNU.Curated;TFactS;TRRUST | 10022869;12374795 | PMID |
| 3 | SMAD4 | JUN | 1.0 | ExTRI;NTNU.Curated;TFactS;TRRUST | 10022869;12374795 | PMID |
| 4 | STAT5A | IL2 | 1.0 | ExTRI | 10022878;11435608;17182565;17911616;22854263;2... | default activation |
| ... | ... | ... | ... | ... | ... | ... |
| 42985 | NFKB | hsa-miR-143-3p | 1.0 | ExTRI | 19472311 | default activation |
| 42986 | AP1 | hsa-miR-206 | 1.0 | ExTRI;GEREDB;NTNU.Curated | 19721712 | PMID |
| 42987 | NFKB | hsa-miR-21 | 1.0 | ExTRI | 20813833;22387281 | default activation |
| 42988 | NFKB | hsa-miR-224-5p | 1.0 | ExTRI | 23474441;23988648 | default activation |
| 42989 | AP1 | hsa-miR-144-3p | 1.0 | ExTRI | 23546882 | default activation |
42990 rows × 6 columns
# Run
tf_acts, tf_padj = dc.mt.ulm(data=data, net=collectri)
# Filter by sign padj
msk = (tf_padj.T < 0.05).iloc[:, 0]
tf_acts = tf_acts.loc[:, msk]
tf_acts
| APEX1 | ARID1A | ARID4B | ARNT | ASXL1 | ATF6 | BARX2 | BCL11A | BCL11B | BMAL2 | ... | TBX10 | TCF21 | TFAP2C | TP53 | VEZF1 | WWTR1 | ZBTB33 | ZEB2 | ZNF804A | ZXDC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| treatment.vs.control | -2.659861 | -3.917514 | -2.807826 | 3.172495 | 3.746244 | 2.70642 | 5.357512 | 2.64909 | -4.204186 | 3.868746 | ... | -3.7051 | 6.162749 | -2.580217 | -3.576216 | 4.207967 | -3.967803 | 3.237428 | 5.790396 | 3.365598 | -2.734615 |
1 rows × 141 columns
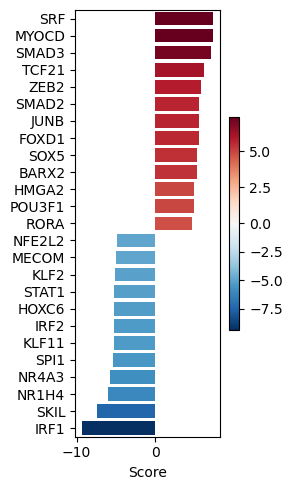
dc.pl.barplot(data=tf_acts, name="treatment.vs.control", top=25, figsize=(3, 5))
Estimation of Receptor activities with RIDDEN#
Now, we will use RIDDEN to estimate receptor activities. Here we know that the cells were treated with TGF-β, but we can assume that in general, this information might not be known. Let’s use RIDDEN with Decoupler to find out, from gene expression alone, which receptors seem to be responsible of the downstream changes in gene expression.
Barsi, S., Varga, E., Dimitrov, D., Saez-Rodriguez, J., Hunyady, L., & Szalai, B. (2025). RIDDEN: Data-driven inference of receptor activity from transcriptomic data. PLOS Computational Biology, 21(6), e1013188. https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1013188
# We obtain ligand-receptor interactions from Omnipath, and we keep only the receptors
# This is our list of a prior potential receptors from which we will infer the network
unique_receptors = set(op.interactions.LigRecExtra.get(genesymbols=True)["target_genesymbol"].values.tolist())
len(unique_receptors)
1201
# We load the RIDDEN matrix
df_ridden = pd.read_csv(
"https://github.com/basvaat/RIDDEN_tool/raw/aa3c9d9880f135e95a079865ee20ebec984cf54d/ridden_model/ridden_model_matrix.csv",
index_col=0,
)
df_ridden
| GNPDA1 | CDH3 | HDAC6 | PARP2 | MAMLD1 | DNAJB6 | SMC4 | ABCC5 | ABCB6 | DNM1L | ... | NCAPD2 | PAN2 | LPGAT1 | KIF14 | CDC25A | CDC25B | OXSR1 | MVP | CDC42 | DMTF1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CALCRL | -0.009687 | -0.007085 | 0.161641 | -0.088799 | 0.141184 | 0.206650 | -0.077551 | 0.089438 | 0.052901 | -0.097550 | ... | -0.029438 | 0.093616 | -0.111194 | 0.055189 | -0.267147 | -0.132507 | 0.075775 | 0.206272 | -0.086620 | 0.089023 |
| IGF1R | 0.186149 | -0.019531 | -0.226755 | 0.241395 | -0.006143 | -0.195346 | -0.074546 | -0.110967 | -0.093491 | 0.144233 | ... | -0.092025 | -0.249430 | -0.090110 | -0.148717 | 0.507459 | -0.383608 | 0.080747 | -0.325099 | 0.122792 | -0.085241 |
| TEK | -0.184470 | 0.103735 | -0.178644 | 0.217038 | -0.030282 | -0.098075 | 0.457752 | 0.060260 | 0.101412 | 0.249132 | ... | -0.022321 | -0.144688 | -0.008170 | 0.418425 | 0.345027 | 0.257878 | 0.283288 | -0.180285 | 0.361584 | 0.121627 |
| GCGR | 0.154128 | -0.062489 | 0.193690 | 0.018437 | 0.037480 | 0.053541 | 0.120568 | 0.101133 | 0.055264 | -0.231345 | ... | -0.074465 | 0.546507 | -0.077048 | 0.118103 | 0.106227 | -0.102328 | -0.023940 | -0.072013 | 0.026697 | 0.201512 |
| AXL | -0.575718 | 0.078760 | -0.014661 | 0.292999 | 0.070583 | -0.012008 | 0.039746 | 0.006026 | 0.060853 | 0.119499 | ... | 0.236579 | -0.145577 | -0.109871 | 0.046791 | 0.301887 | -0.046162 | -0.022249 | -0.197795 | 0.319452 | 0.002319 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| LAT | -0.090900 | -0.085613 | -0.050680 | 0.071466 | -0.020198 | -0.005307 | 0.152670 | 0.605020 | 0.339265 | -0.044672 | ... | 0.077842 | 0.541145 | -0.112621 | 0.378760 | -0.020636 | -0.188372 | -0.031565 | -0.447521 | 0.152605 | 0.233283 |
| KIR3DL2 | -0.113160 | -0.078494 | 0.076545 | -0.078937 | 0.243577 | -0.189946 | 0.286184 | 0.039433 | -0.174081 | -0.109293 | ... | -0.148066 | 0.118362 | 0.199176 | 0.109609 | 0.091345 | 0.243448 | 0.109597 | 0.032553 | 0.254494 | 0.058646 |
| ROR1 | -0.090646 | 0.012197 | -0.271497 | -0.158861 | 0.256878 | -0.078914 | -0.364736 | -0.012256 | -0.192445 | -0.670970 | ... | -0.005142 | -0.096561 | -0.262883 | -0.399374 | -0.109447 | -0.239205 | -0.257403 | 0.030898 | 0.098747 | 0.123366 |
| AGER | 0.020215 | 0.288864 | 0.214776 | -0.022412 | -0.038031 | -0.152819 | 0.157402 | 0.367379 | -0.038862 | -0.294257 | ... | -0.198762 | 0.227099 | 0.167598 | 0.154016 | 0.059484 | 0.124841 | 0.020183 | 0.083234 | 0.290658 | 0.194672 |
| LPAR4 | -0.207898 | -0.260550 | 0.091162 | 0.236077 | 0.242604 | -0.122191 | 0.661206 | -0.262016 | 0.296903 | -0.370393 | ... | -0.144404 | -0.132523 | 1.057903 | 0.216050 | 0.265133 | 0.621863 | 0.151718 | -0.158971 | 0.196567 | -0.274069 |
229 rows × 978 columns
df_receptor_de = data.loc[:, data.columns.intersection(df_ridden.columns)]
df_receptor_de
| CDC25B | CCNB2 | ABCC5 | NPDC1 | AGL | GMNN | BLCAP | ISOC1 | SLC35B1 | PAK1 | ... | HMGCR | LAMA3 | FAM57A | SSBP2 | CXCL2 | GTPBP8 | TRIB3 | HDAC2 | LGALS8 | BIRC5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| treatment.vs.control | -8.391308 | 6.554248 | -4.139615 | -2.506713 | 0.299272 | 6.582295 | -2.918605 | -9.658493 | 3.163861 | 3.969934 | ... | 7.125527 | -3.862645 | 7.445228 | -8.977077 | -6.753168 | -5.144084 | 2.988088 | 5.638864 | -1.495224 | 6.237914 |
1 rows × 923 columns
ridden_pkn = df_ridden.reset_index().melt(id_vars="index")
ridden_pkn.columns = ["source", "target", "weight"]
ridden_pkn
| source | target | weight | |
|---|---|---|---|
| 0 | CALCRL | GNPDA1 | -0.009687 |
| 1 | IGF1R | GNPDA1 | 0.186149 |
| 2 | TEK | GNPDA1 | -0.184470 |
| 3 | GCGR | GNPDA1 | 0.154128 |
| 4 | AXL | GNPDA1 | -0.575718 |
| ... | ... | ... | ... |
| 223957 | LAT | DMTF1 | 0.233283 |
| 223958 | KIR3DL2 | DMTF1 | 0.058646 |
| 223959 | ROR1 | DMTF1 | 0.123366 |
| 223960 | AGER | DMTF1 | 0.194672 |
| 223961 | LPAR4 | DMTF1 | -0.274069 |
223962 rows × 3 columns
# Number of receptors in RIDDEN
len(ridden_pkn.source.unique())
229
# Run receptor enrichment with ULM
pw_acts, pw_padj = dc.mt.ulm(data=df_receptor_de, net=ridden_pkn)
df_ridden_stats = pd.concat([pw_acts, pw_padj]).T
df_ridden_stats.columns = ["activity", "padj"]
df_ridden_stats
| activity | padj | |
|---|---|---|
| ABCA1 | -3.200361 | 0.005805 |
| ACKR3 | 0.021177 | 0.987421 |
| ACTR2 | -0.719527 | 0.610665 |
| ACVR1 | 1.328386 | 0.322313 |
| ACVR1B | 3.479168 | 0.002621 |
| ... | ... | ... |
| TRAF2 | -3.720026 | 0.001273 |
| TYRO3 | -2.529414 | 0.034332 |
| UTS2R | -4.141094 | 0.000332 |
| VIPR1 | 1.310146 | 0.327957 |
| XCR1 | -1.241386 | 0.341352 |
229 rows × 2 columns
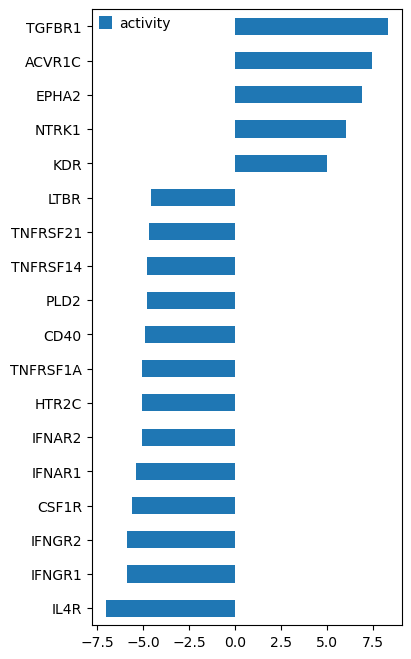
# We inferred from gene expression that TGFBR1 is the most active receptor
df_ridden_stats[df_ridden_stats.padj <= 0.0001][["activity"]].sort_values(by="activity", ascending=True).plot.barh(
figsize=(4, 8)
)
<Axes: >
Inferring intracellular signalling network with CARNIVAL and CORNETO#
CORNETO is a unified framework for knowledge-driven network inference. It includes a very flexible implementation of CARNIVAL that expands its original capabilities. We will see how to use it under different assumptions to extract a network from a prior knowledge network and a set of potential receptors + our estimated TFs
cn.info()
|
|
|
from corneto.methods.future import CarnivalFlow
CarnivalFlow.show_references()
- Pablo Rodriguez-Mier, Martin Garrido-Rodriguez, Attila Gabor, Julio Saez-Rodriguez. Unified knowledge-driven network inference from omics data. bioRxiv, pp. 10 (2024).
- Anika Liu, Panuwat Trairatphisan, Enio Gjerga, Athanasios Didangelos, Jonathan Barratt, Julio Saez-Rodriguez. From expression footprints to causal pathways: contextualizing large signaling networks with CARNIVAL. NPJ systems biology and applications, Vol. 5, No. 1, pp. 40 (2019).
# We get only interactions from SIGNOR http://signor.uniroma2.it/
pkn = op.interactions.OmniPath.get(databases=["SIGNOR"], genesymbols=True)
pkn = pkn[pkn.consensus_direction == True]
pkn.head()
| source | target | source_genesymbol | target_genesymbol | is_directed | is_stimulation | is_inhibition | consensus_direction | consensus_stimulation | consensus_inhibition | curation_effort | references | sources | n_sources | n_primary_sources | n_references | references_stripped | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Q13976 | Q13507 | PRKG1 | TRPC3 | True | False | True | True | False | True | 9 | HPRD:14983059;KEA:14983059;ProtMapper:14983059... | HPRD;HPRD_KEA;HPRD_MIMP;KEA;MIMP;PhosphoPoint;... | 15 | 8 | 2 | 14983059;16331690 |
| 1 | Q13976 | Q9HCX4 | PRKG1 | TRPC7 | True | True | False | True | True | False | 3 | SIGNOR:21402151;TRIP:21402151;iPTMnet:21402151 | SIGNOR;TRIP;iPTMnet | 3 | 3 | 1 | 21402151 |
| 2 | Q13438 | Q9HBA0 | OS9 | TRPV4 | True | True | True | True | True | True | 3 | HPRD:17932042;SIGNOR:17932042;TRIP:17932042 | HPRD;SIGNOR;TRIP | 3 | 3 | 1 | 17932042 |
| 3 | P18031 | Q9H1D0 | PTPN1 | TRPV6 | True | False | True | True | False | True | 11 | DEPOD:15894168;DEPOD:17197020;HPRD:15894168;In... | DEPOD;HPRD;IntAct;Lit-BM-17;SIGNOR;SPIKE_LC;TRIP | 7 | 6 | 2 | 15894168;17197020 |
| 4 | P63244 | Q9BX84 | RACK1 | TRPM6 | True | False | True | True | False | True | 2 | SIGNOR:18258429;TRIP:18258429 | SIGNOR;TRIP | 2 | 2 | 1 | 18258429 |
pkn["interaction"] = pkn["is_stimulation"].astype(int) - pkn["is_inhibition"].astype(int)
sel_pkn = pkn[["source_genesymbol", "interaction", "target_genesymbol"]]
sel_pkn
| source_genesymbol | interaction | target_genesymbol | |
|---|---|---|---|
| 0 | PRKG1 | -1 | TRPC3 |
| 1 | PRKG1 | 1 | TRPC7 |
| 2 | OS9 | 0 | TRPV4 |
| 3 | PTPN1 | -1 | TRPV6 |
| 4 | RACK1 | -1 | TRPM6 |
| ... | ... | ... | ... |
| 61542 | APC_PUF60_SIAH1_SKP1_TBL1X | -1 | CTNNB1 |
| 61543 | MAP2K6 | 1 | MAPK10 |
| 61544 | PRKAA1 | 1 | TP53 |
| 61545 | CNOT1_CNOT10_CNOT11_CNOT2_CNOT3_CNOT4_CNOT6_CN... | -1 | NANOS2 |
| 61546 | WNT16 | 1 | FZD3 |
60921 rows × 3 columns
# We create the CORNETO graph by importing the edges and interaction
from corneto.io import load_graph_from_sif_tuples
G = load_graph_from_sif_tuples([(r[0], r[1], r[2]) for _, r in sel_pkn.iterrows() if r[1] != 0])
G.shape
(5442, 60034)
# As measurements, we take the estimated TFs, we will filter out TFs with p-val > 0.001
significant_tfs = tf_acts[tf_padj <= 0.001].T.dropna().sort_values(by="treatment.vs.control", ascending=False)
significant_tfs
| treatment.vs.control | |
|---|---|
| SRF | 7.384275 |
| MYOCD | 7.346561 |
| SMAD3 | 7.088023 |
| TCF21 | 6.162749 |
| ZEB2 | 5.790396 |
| SMAD2 | 5.617299 |
| JUNB | 5.613301 |
| FOXD1 | 5.569131 |
| SOX5 | 5.388260 |
| BARX2 | 5.357512 |
| HMGA2 | 4.920654 |
| POU3F1 | 4.906394 |
| RORA | 4.751216 |
| SMAD4 | 4.442445 |
| OVOL1 | 4.282917 |
| MEF2A | 4.234915 |
| FGF2 | 4.210021 |
| VEZF1 | 4.207967 |
| EGR4 | 4.112604 |
| SMAD5 | -4.006291 |
| CIITA | -4.135616 |
| NFKBIB | -4.156422 |
| REL | -4.167478 |
| PITX3 | -4.200405 |
| BCL11B | -4.204186 |
| IRF3 | -4.275299 |
| PITX1 | -4.343037 |
| PARK7 | -4.447875 |
| KLF8 | -4.469565 |
| DNMT3A | -4.642689 |
| RELB | -4.684594 |
| NFE2L2 | -4.913963 |
| MECOM | -4.945115 |
| KLF2 | -5.096991 |
| STAT1 | -5.192426 |
| HOXC6 | -5.261645 |
| IRF2 | -5.272422 |
| KLF11 | -5.272551 |
| SPI1 | -5.425817 |
| NR4A3 | -5.726681 |
| NR1H4 | -6.059037 |
| SKIL | -7.437322 |
| IRF1 | -9.362766 |
# We keep only the ones in the PKN graph
measurements = significant_tfs.loc[significant_tfs.index.intersection(G.V)].to_dict()["treatment.vs.control"]
measurements
{'SRF': 7.384274933753678,
'MYOCD': 7.346560585692566,
'SMAD3': 7.088022567967861,
'ZEB2': 5.790395603340423,
'SMAD2': 5.617299171561388,
'JUNB': 5.613301413598558,
'HMGA2': 4.920654205164735,
'POU3F1': 4.9063937479035795,
'RORA': 4.751215803623851,
'SMAD4': 4.442444690531756,
'MEF2A': 4.234915033987421,
'FGF2': 4.210020918905277,
'SMAD5': -4.006290782113948,
'CIITA': -4.135615580532372,
'NFKBIB': -4.156422100656065,
'REL': -4.167478417685659,
'PITX3': -4.200405283105377,
'IRF3': -4.275299453731299,
'PITX1': -4.343036884101653,
'KLF8': -4.469565287654229,
'DNMT3A': -4.642688562638021,
'RELB': -4.684594362576203,
'NFE2L2': -4.913963130388188,
'MECOM': -4.9451147439384044,
'STAT1': -5.19242581697902,
'HOXC6': -5.261644928875645,
'IRF2': -5.272422064497416,
'KLF11': -5.272550840567249,
'SPI1': -5.425816853074546,
'NR4A3': -5.726680520718154,
'NR1H4': -6.059037198788599,
'SKIL': -7.437321830844388,
'IRF1': -9.362766415720282}
"TGFBR1" in G.V
True
# Here we pass the receptors. We're going to use the top receptor inferred by RIDDEN
# (TGFBR1)
inputs = {"TGFBR1": 1} # 1=up, -1=down
inputs
{'TGFBR1': 1}
# Create the dataset in standard format
carnival_data = dict()
for inp, v in inputs.items():
carnival_data[inp] = dict(value=v, role="input", mapping="vertex")
for out, v in measurements.items():
carnival_data[out] = dict(value=v, role="output", mapping="vertex")
data = cn.Data.from_cdict({"sample1": carnival_data})
data
Data(n_samples=1, n_feats=[34])
CARNIVAL#
We will use now the CARNIVAL, as implemented with CORNETO, with a penalty to regularize the solution. For hypothesis exploration, we can try different values and manually inspect the solutions. We are going to penalize also the selection of indirect rules, to simplify the solution. These rules are:
A -> B in the PKN, and we observe B is downregulated, we explain it with downregulation of its upstream gene A
A -| B in the PKN, and we observe B is upregulated, we explain it with downregulation of A
carnival = CarnivalFlow(lambda_reg=1.0, indirect_rule_penalty=10)
P = carnival.build(G, data)
P.expr
Unreachable vertices for sample: 0
{'_flow': _flow: Variable((3251,), _flow),
'const0x41332f448f64593': const0x41332f448f64593: Constant(CONSTANT, NONNEGATIVE, (937, 3251)),
'const0xd5dbd53619f708b': const0xd5dbd53619f708b: Constant(CONSTANT, NONNEGATIVE, (937, 3251)),
'edge_inhibits': edge_inhibits: Variable((3251, 1), edge_inhibits, boolean=True),
'edge_activates': edge_activates: Variable((3251, 1), edge_activates, boolean=True),
'_dag_layer': _dag_layer: Variable((937, 1), _dag_layer),
'flow': _flow: Variable((3251,), _flow),
'vertex_value': Expression(AFFINE, UNKNOWN, (937, 1)),
'vertex_activated': Expression(AFFINE, NONNEGATIVE, (937, 1)),
'vertex_inhibited': Expression(AFFINE, NONNEGATIVE, (937, 1)),
'edge_value': Expression(AFFINE, UNKNOWN, (3251, 1)),
'edge_has_signal': Expression(AFFINE, NONNEGATIVE, (3251, 1)),
'vertex_max_depth': _dag_layer: Variable((937, 1), _dag_layer)}
P.solve(solver="highs", max_seconds=60, verbosity=1);
===============================================================================
CVXPY
v1.6.6
===============================================================================
-------------------------------------------------------------------------------
Compilation
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
Numerical solver
-------------------------------------------------------------------------------
Running HiGHS 1.11.0 (git hash: 364c83a): Copyright (c) 2025 HiGHS under MIT licence terms
MIP has 30607 rows; 10690 cols; 108040 nonzeros; 6502 integer variables (6502 binary)
Coefficient ranges:
Matrix [1e+00, 9e+02]
Cost [1e+00, 2e+01]
Bound [1e+00, 1e+00]
RHS [1e+00, 1e+03]
Presolving model
17788 rows, 10299 cols, 91260 nonzeros 0s
12833 rows, 9086 cols, 69235 nonzeros 0s
12455 rows, 9011 cols, 68752 nonzeros 0s
Solving MIP model with:
12455 rows
9011 cols (5625 binary, 0 integer, 0 implied int., 3386 continuous, 0 domain fixed)
68752 nonzeros
Src: B => Branching; C => Central rounding; F => Feasibility pump; J => Feasibility jump;
H => Heuristic; L => Sub-MIP; P => Empty MIP; R => Randomized rounding; Z => ZI Round;
I => Shifting; S => Solve LP; T => Evaluate node; U => Unbounded; X => User solution;
z => Trivial zero; l => Trivial lower; u => Trivial upper; p => Trivial point
Nodes | B&B Tree | Objective Bounds | Dynamic Constraints | Work
Src Proc. InQueue | Leaves Expl. | BestBound BestSol Gap | Cuts InLp Confl. | LpIters Time
J 0 0 0 0.00% -inf 1 Large 0 0 0 0 0.6s
0 0 0 0.00% -35.76172711 1 3676.17% 0 0 0 924 0.7s
C 0 0 0 0.00% -31.47852215 -1.758607953 1689.97% 169 24 0 1062 1.5s
L 0 0 0 0.00% -31.47852215 -30.33661578 3.76% 280 35 0 1112 2.5s
62.0% inactive integer columns, restarting
Model after restart has 1325 rows, 2777 cols (204 bin., 0 int., 0 impl., 2573 cont., 0 dom.fix.), and 8468 nonzeros
0 0 0 0.00% -31.47852215 -30.33661578 3.76% 15 0 0 5669 3.1s
0 0 0 0.00% -31.47852215 -30.33661578 3.76% 16 5 0 6412 3.1s
57.8% inactive integer columns, restarting
Model after restart has 930 rows, 2595 cols (81 bin., 0 int., 0 impl., 2514 cont., 0 dom.fix.), and 6944 nonzeros
0 0 0 0.00% -31.00328245 -30.33661578 2.20% 8 0 0 8365 3.3s
0 0 0 0.00% -31.00328245 -30.33661578 2.20% 8 5 1 8932 3.3s
7.4% inactive integer columns, restarting
Model after restart has 878 rows, 2570 cols (68 bin., 0 int., 0 impl., 2502 cont., 0 dom.fix.), and 6788 nonzeros
0 0 0 0.00% -30.47852215 -30.33661578 0.47% 16 0 0 10659 3.5s
0 0 0 0.00% -30.47852215 -30.33661578 0.47% 16 14 2 10964 3.5s
13.2% inactive integer columns, restarting
Model after restart has 829 rows, 2548 cols (52 bin., 0 int., 0 impl., 2496 cont., 0 dom.fix.), and 6636 nonzeros
0 0 0 0.00% -30.47852215 -30.33661578 0.47% 9 0 0 11860 3.6s
0 0 0 0.00% -30.47852215 -30.33661578 0.47% 9 5 2 12178 3.6s
1 0 1 100.00% -30.33661578 -30.33661578 0.00% 313 36 15 13592 3.8s
Solving report
Status Optimal
Primal bound -30.3366157837
Dual bound -30.3366157837
Gap 0% (tolerance: 0.01%)
P-D integral 47.8825450825
Solution status feasible
-30.3366157837 (objective)
0 (bound viol.)
0 (int. viol.)
0 (row viol.)
Timing 3.76 (total)
0.00 (presolve)
0.00 (solve)
0.00 (postsolve)
Max sub-MIP depth 5
Nodes 1
Repair LPs 0 (0 feasible; 0 iterations)
LP iterations 13592 (total)
0 (strong br.)
1033 (separation)
9661 (heuristics)
-------------------------------------------------------------------------------
Summary
-------------------------------------------------------------------------------
# Error for sample is 0, meaning that all reachable TFs (from receptors) are correctly explained
for o in P.objectives:
print(o.name, "->", o.value)
error_sample1_0 -> 65.03395318114363
penalty_indirect_rules_0 -> [0.]
regularization_edge_has_signal -> 28.0
# We extract the selected edges
sol_edges = np.flatnonzero(np.abs(P.expr.edge_value.value) > 0.5)
carnival.processed_graph.plot_values(
vertex_values=P.expr.vertex_value.value,
edge_values=P.expr.edge_value.value,
edge_indexes=sol_edges,
)
# Extracting the solution graph
G_sol = carnival.processed_graph.edge_subgraph(sol_edges)
G_sol.shape
(28, 28)
pd.DataFrame(
P.expr.vertex_value.value,
index=carnival.processed_graph.V,
columns=["node_activity"],
)
| node_activity | |
|---|---|
| P03231_UBA52 | 0.0 |
| GNAI1 | 0.0 |
| CDC42 | 0.0 |
| RPS6KA5 | 0.0 |
| P03186_UBB | 0.0 |
| ... | ... |
| SET | 0.0 |
| SYNJ1 | 0.0 |
| MAP2K5 | 0.0 |
| IFITM3 | 0.0 |
| CDK2 | 0.0 |
937 rows × 1 columns
pd.DataFrame(P.expr.edge_value.value, index=carnival.processed_graph.E, columns=["edge_activity"])
| edge_activity | ||
|---|---|---|
| (SMAD3) | (MYOD1) | 0.0 |
| (GRK2) | (BDKRB2) | 0.0 |
| (MAPK14) | (MAPKAPK2) | 1.0 |
| (DEPTOR_EEF1A1_MLST8_MTOR_PRR5_RICTOR) | (FBXW8) | 0.0 |
| (SLK) | (MAP3K5) | 0.0 |
| ... | ... | ... |
| (JUNB) | () | 0.0 |
| (SRF) | () | 0.0 |
| (ZEB2) | () | 0.0 |
| (SMAD2) | () | 0.0 |
| () | (TGFBR1) | 1.0 |
3251 rows × 1 columns
Saving the processed dataset#
cn.GraphData(G, data).save("data/carnival_transcriptomics_dataset")
