Exploring alternative solutions with \(\epsilon\)-perturbation sampling#

CORNETO includes a basic ε-Perturbation Sampling method for uncovering near-optimal alternatives. Starting from the optimal solution, it applies small random “jitter” to a selected variable, re-solves the model, and retains only those samples whose original objectives remain within a user-specified tolerance. The result is a collection of feasible alternatives that highlights which components are fixed versus flexible.

We will illustrate this process using a simple example of a network inference problem with CARNIVAL, using the data from the CARNIVAL transcriptomics tutorial.

NOTE: This notebook uses gurobi as the solver and cvxpy as the backend to accelerate the generation of alternative solutions using the warm_start option from cvxpy

import numpy as np
import pandas as pd

import corneto as cn

cn.enable_logging()
cn.info()
Installed version:v1.0.0.dev41+774fa03b
Available backends:CVXPY v1.6.6, PICOS v2.6.1
Default backend (corneto.opt):CVXPY
Installed solvers:CLARABEL, COPT, CVXOPT, GLPK, GLPK_MI, GUROBI, HIGHS, OSQP, PROXQP, SCIP, SCIPY, SCS
Graphviz version:v0.20.3
Installed path:/Users/pablorodriguezmier/Documents/work/repos/pablormier/corneto/corneto
Repository:https://github.com/saezlab/corneto
 
# Load dataset from tutorial
dataset = cn.GraphData.load("data/carnival_transcriptomics_dataset.zip")

from corneto.methods.future import CarnivalFlow

m = CarnivalFlow(lambda_reg=0.1)
P = m.build(dataset.graph, dataset.data)
P.objectives

Unreachable vertices for sample: 0

[error_sample1_0: Expression(AFFINE, UNKNOWN, ()),
 regularization_edge_has_signal: Expression(AFFINE, NONNEGATIVE, ())]

# We will sample solutions by perturbing the edge_has_signal variable
P.expr

{'edge_activates': edge_activates: Variable((3251, 1), edge_activates, boolean=True),
 '_dag_layer': _dag_layer: Variable((937, 1), _dag_layer),
 '_flow': _flow: Variable((3251,), _flow),
 'edge_inhibits': edge_inhibits: Variable((3251, 1), edge_inhibits, boolean=True),
 'const0xf61164977a1fb6a': const0xf61164977a1fb6a: Constant(CONSTANT, NONNEGATIVE, (937, 3251)),
 'const0x1d35f8e3c1977ecb': const0x1d35f8e3c1977ecb: Constant(CONSTANT, NONNEGATIVE, (937, 3251)),
 'flow': _flow: Variable((3251,), _flow),
 'vertex_value': Expression(AFFINE, UNKNOWN, (937, 1)),
 'vertex_activated': Expression(AFFINE, NONNEGATIVE, (937, 1)),
 'vertex_inhibited': Expression(AFFINE, NONNEGATIVE, (937, 1)),
 'edge_value': Expression(AFFINE, UNKNOWN, (3251, 1)),
 'edge_has_signal': Expression(AFFINE, NONNEGATIVE, (3251, 1)),
 'vertex_max_depth': _dag_layer: Variable((937, 1), _dag_layer)}

# These are the original objectives of the problem
for o in P.objectives:
    print(o.name)

error_sample1_0
regularization_edge_has_signal

Edge-Based Perturbation#

First, we’ll sample solutions by perturbing the edge variables. This allows us to explore alternative network topologies where different edges might be selected.

from corneto.methods.sampler import sample_alternative_solutions

# Create a fresh model
m = CarnivalFlow(lambda_reg=0.1)
P = m.build(dataset.graph, dataset.data)

# NOTE: The sampler modifies the original P problem
results = sample_alternative_solutions(
    P,
    "edge_has_signal",
    percentage=0.10,
    scale=0.05,
    rel_opt_tol=0.10,
    max_samples=30,
    solver_kwargs=dict(solver="gurobi", max_seconds=300, IntegralityFocus=1),
)

Unreachable vertices for sample: 0
Set parameter Username
Set parameter LicenseID to value 2593994
Academic license - for non-commercial use only - expires 2025-12-02

edges = np.squeeze(results["edge_value"]).T
df_sols = pd.DataFrame(edges, index=m.processed_graph.E).astype(int)
print(f"Generated {df_sols.shape[1]} alternative solutions")
df_sols.head()

Generated 31 alternative solutions
0 1 2 3 4 5 6 7 8 9 ... 21 22 23 24 25 26 27 28 29 30
(SMAD3) (MYOD1) 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
(GRK2) (BDKRB2) 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
(MAPK14) (MAPKAPK2) 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
(DEPTOR_EEF1A1_MLST8_MTOR_PRR5_RICTOR) (FBXW8) 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
(SLK) (MAP3K5) 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0

5 rows × 31 columns

# Analyze variability in edge selection
df_var = pd.concat([df_sols.mean(axis=1), df_sols.std(axis=1)], axis=1)
df_var.columns = ["mean", "std"]
print("Edges with highest variability across solutions:")
df_var.sort_values(by="std", ascending=False).head(50).sort_values(by="mean")

Edges with highest variability across solutions:
mean std
(JUN) (SPI1) -0.741935 0.444803
(PRKCA) (NFE2L2) -0.741935 0.444803
(MAPK1) (MYC) -0.709677 0.461414
(TBK1) (IRF3) -0.677419 0.475191
(MAPK8) (STAT1) -0.645161 0.486373
(SKI) (SMAD5) -0.580645 0.501610
(CDK1) (TP53) -0.548387 0.505879
(NFKB1_RELA) (EGR1) -0.516129 0.508001
(GSK3B) (PRKCE) -0.516129 0.508001
(TICAM2) (TICAM1) -0.516129 0.508001
(PRKCE) (TICAM2) -0.516129 0.508001
(PPP1CA) (MAPK1) -0.516129 0.508001
(TRAF2) (TICAM1) -0.483871 0.508001
(RELA) (EGR1) -0.483871 0.508001
(PPP2CA) (TRAF2) -0.451613 0.505879
(MAPK1) (JUN) -0.451613 0.505879
(SMURF2) (SMAD5) -0.419355 0.501610
(KHSRP) (SRC) -0.387097 0.495138
(CDK1) (AKAP12) -0.387097 0.495138
(MAPK14) (KHSRP) -0.387097 0.495138
(GSK3B) (NFKB1_RELA) -0.387097 0.495138
(AKAP12) (PRKCA) -0.387097 0.495138
(PPP2CA) (MAPK1) -0.354839 0.486373
(PRKCD) (MAPK8) -0.354839 0.486373
(PPP2CA) (PRKCD) -0.290323 0.461414
(PHLPP1) (PRKCA) -0.290323 0.461414
(MAPK8) (MYC) -0.258065 0.444803
(GSK3B) (RELA) -0.258065 0.444803
(SRC) (PDPK1) -0.258065 0.444803
(PRKCD) (NFE2L2) -0.258065 0.444803
(MAPK8) (IRF3) -0.193548 0.401610
(MAP3K7) (MAP2K6) 0.225806 0.425024
(MAP2K6) (MAPK14) 0.225806 0.425024
(MAPK14) (CDKN1A) 0.225806 0.425024
(SMAD3) 0.258065 0.444803
(GSK3B) (PHLPP1) 0.290323 0.461414
(MAP3K7) (MAP2K3) 0.322581 0.475191
(MAP2K3) (MAPK14) 0.322581 0.475191
(SMAD3) (SMAD4) 0.322581 0.475191
(SRC) (PPP2CA) 0.387097 0.495138
(MAPK8) (AIMP1) 0.387097 0.495138
(AIMP1) (SMURF2) 0.387097 0.495138
(MAP2K4) (MAPK14) 0.419355 0.501610
(MAP3K7) (MAP2K4) 0.419355 0.501610
(CDK1) (PPP1CA) 0.516129 0.508001
(AKT1) (SKI) 0.580645 0.501610
(GSK3B) (CDKN1A) 0.612903 0.495138
(SMAD2) (SMAD4) 0.677419 0.475191
(PML) (SMAD3) 0.709677 0.461414
(MAPK8) (CTBP1) 0.774194 0.425024

Vertex-Based Perturbation#

We can do the same but perturbing the vertices instead of the edges. This approach can highlight alternative sets of vertices that are consistent with the data.

# Create a fresh model
m = CarnivalFlow(lambda_reg=0.1)
P = m.build(dataset.graph, dataset.data)

# Sample solutions by perturbing vertex_value
results = sample_alternative_solutions(
    P,
    "vertex_value",
    percentage=0.10,
    scale=0.05,
    rel_opt_tol=0.10,
    max_samples=30,
    solver_kwargs=dict(solver="gurobi", max_seconds=300, IntegralityFocus=1),
)

Unreachable vertices for sample: 0

vertex_values = np.squeeze(results["vertex_value"]).T
vertex_values.shape

(937, 31)

# Analyze vertex-based results
df_vertex_val = pd.DataFrame(vertex_values, index=m.processed_graph.V).astype(int)
print(f"Generated {df_vertex_val.shape[1]} alternative solutions")
df_vertex_val.head()

Generated 31 alternative solutions
0 1 2 3 4 5 6 7 8 9 ... 21 22 23 24 25 26 27 28 29 30
CDK6 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
PIK3CG 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
SPRY1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
P59595_UBB 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
APAF1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0

5 rows × 31 columns

# Focus on signaling proteins with no measurement data
df_sig_prot_pred = df_vertex_val.loc[df_vertex_val.index.difference(dataset.data.query.pluck_features())]
df_sig_prot_pred.head()
0 1 2 3 4 5 6 7 8 9 ... 21 22 23 24 25 26 27 28 29 30
AAK1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
ABI1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
ABL1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
ABRAXAS1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
ACAT1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0

5 rows × 31 columns

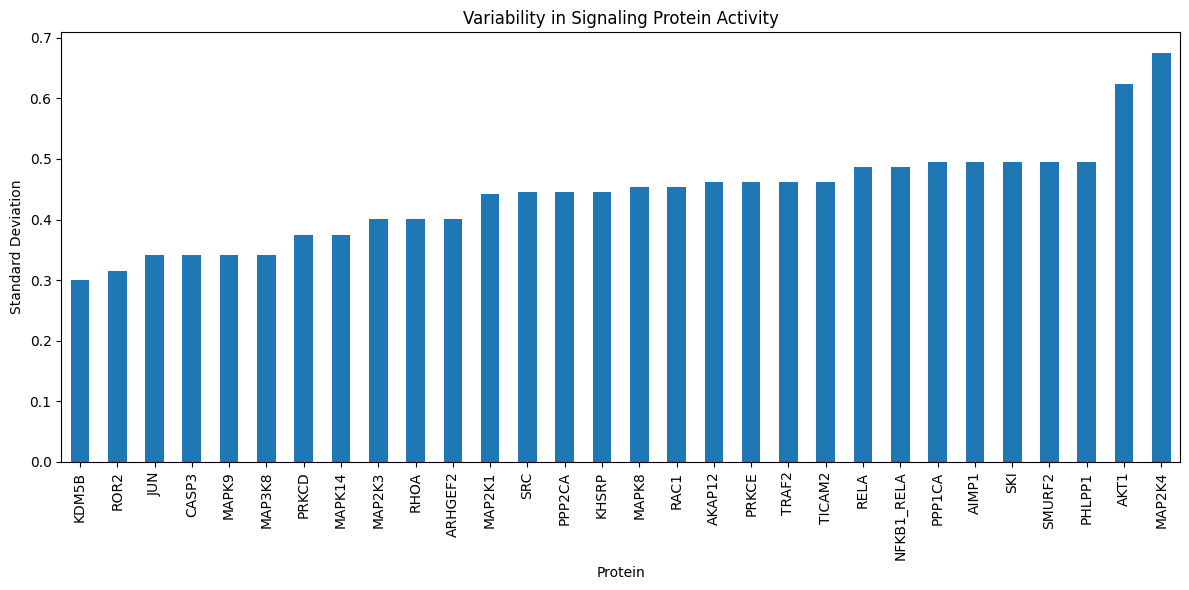
# Visualize the variability in predicted signaling protein activities
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))
df_sig_prot_pred.std(axis=1).sort_values().tail(30).plot.bar(title="Variability in Signaling Protein Activity")
plt.xlabel("Protein")
plt.ylabel("Standard Deviation")
plt.tight_layout()
plt.show()
../../_images/f9def52fe3b10b5fc54d188b1b238b6d0184aa61490a3099cac8213248483d9f.png