Knowledge-primed Neural Networks (KPNNs) for single cell data#

In this tutorial we will show how CORNETO can be used to build custom neural network architectures informed by prior knowledge. We will see how to implement a knowledge-primed neural network1. We will use the single cell data from the publication “Knowledge-primed neural networks enable biologically interpretable deep learning on single-cell sequencing data”, from Nikolaus Fortelny & Christoph Bock, where they used a single-cell RNA-seq dataset they previously generated2, which measures cellular responses to T cell receptor (TCR) stimulation in a standardized in vitro model. The dataset was chosen due to the TCR signaling pathway’s complexity and its well-characterized role in orchestrating transcriptional responses to antigen detection in T cells.

Why CORNETO?#

In the original publication, authors built a KPNN by searching on databases, building a Direct Acyclic Graph (DAG) by running shortest paths from TCR receptor to genes. However, this approach is not optimal. CORNETO, thanks to its advanced capabilities for modeling and optimization on networks, provides methods to automatically find DAG architectures in an optimal way.

In addition to this, CORNETO provides methods to build DAG NN architectures with ease using Keras +3, making KPNN implementation very flexible and interoperable with backends like Pytorch, Tensorflow and JAX.

How does it work?#

Thanks to CORNETO’s building blocks for optimization over networks, we can easily model optimization problems to find DAG architectures from a Prior Knowledge Network. After we have the backbone, we can convert it to a neural network using the utility functions included in CORNETO.

References#

  1. Fortelny, N., & Bock, C. (2020). Knowledge-primed neural networks enable biologically interpretable deep learning on single-cell sequencing data. Genome biology, 21, 1-36.

  2. Datlinger, P., Rendeiro, A. F., Schmidl, C., Krausgruber, T., Traxler, P., Klughammer, J., … & Bock, C. (2017). Pooled CRISPR screening with single-cell transcriptome readout. Nature methods, 14(3), 297-301.

Download and import the single cell dataset#

import os
import tempfile
import urllib.parse
import urllib.request

import numpy as np
import pandas as pd
import scanpy as sc

import corneto as cn

with urllib.request.urlopen("http://kpnn.computational-epigenetics.org/") as response:
    web_input = response.geturl()
print("Effective URL:", web_input)

files = ["TCR_Edgelist.csv", "TCR_ClassLabels.csv", "TCR_Data.h5"]

temp_dir = tempfile.mkdtemp()

# Download files
file_paths = []
for file in files:
    url = urllib.parse.urljoin(web_input, file)
    output_path = os.path.join(temp_dir, file)
    print(f"Downloading {url} to {output_path}")
    try:
        with urllib.request.urlopen(url) as response:
            with open(output_path, "wb") as f:
                f.write(response.read())
        file_paths.append(output_path)
    except Exception as e:
        print(f"Failed to download {url}: {e}")

print("Downloaded files:")
for path in file_paths:
    print(path)

Effective URL: https://medical-epigenomics.org/papers/fortelny2019/
Downloading https://medical-epigenomics.org/papers/fortelny2019/TCR_Edgelist.csv to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp5w2c_81g/TCR_Edgelist.csv
Downloading https://medical-epigenomics.org/papers/fortelny2019/TCR_ClassLabels.csv to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp5w2c_81g/TCR_ClassLabels.csv
Downloading https://medical-epigenomics.org/papers/fortelny2019/TCR_Data.h5 to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp5w2c_81g/TCR_Data.h5
Downloaded files:
/var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp5w2c_81g/TCR_Edgelist.csv
/var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp5w2c_81g/TCR_ClassLabels.csv
/var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp5w2c_81g/TCR_Data.h5

# The data contains also the original network they built with shortest paths.
# We will use it to replicate the study
df_edges = pd.read_csv(file_paths[0])
df_labels = pd.read_csv(file_paths[1])
# Import the 10x data with Scanpy
adata = sc.read_10x_h5(file_paths[2])

df_labels
barcode TCR
0 AAACCTGCACACATGT-1 0
1 AAACCTGCACGTCTCT-1 0
2 AAACCTGTCAATACCG-1 0
3 AAACCTGTCGTGGTCG-1 0
4 AAACGGGTCTGAGTGT-1 0
... ... ...
1730 TTTCCTCGTCATGCCG-2 1
1731 TTTGCGCGTAGCCTCG-2 1
1732 TTTGGTTAGATACACA-2 1
1733 TTTGGTTGTATGAATG-2 1
1734 TTTGGTTTCCAAGTAC-2 1

1735 rows × 2 columns

df_edges
parent child
0 TCR ZAP70
1 ZAP70 MAPK14
2 MAPK14 FOXO3
3 MAPK14 STAT1
4 MAPK14 STAT3
... ... ...
27574 HMGA1 MTRNR2L9_gene
27575 MYB C12orf50_gene
27576 MYB TRPC5OS_gene
27577 SOX2 TRPC5OS_gene
27578 CRTC1 MTRNR2L9_gene

27579 rows × 2 columns

adata.var
gene_ids
DDX11L1 ENSG00000223972
WASH7P ENSG00000227232
MIR6859-2 ENSG00000278267
MIR1302-10 ENSG00000243485
MIR1302-11 ENSG00000274890
... ...
Tcrlibrary_RUNX2_3_gene Tcrlibrary_RUNX2_3_gene
Tcrlibrary_ZAP70_1_gene Tcrlibrary_ZAP70_1_gene
Tcrlibrary_ZAP70_2_gene Tcrlibrary_ZAP70_2_gene
Tcrlibrary_ZAP70_3_gene Tcrlibrary_ZAP70_3_gene
Cas9_blast_gene Cas9_blast_gene

64370 rows × 1 columns

# We can normalize the data, however, it is better to avoid
# preprocessing the whole dataset before splitting in training and test
# to avoid data leakage.
# NOTE: Normalization can be done inside the cross-val loop
# sc.pp.normalize_total(adata, target_sum=1e6)

# Log-transform the data does not leak data as it does not estimate anything
sc.pp.log1p(adata)

adata.obs
AAACCTGAGAAACCAT-1
AAACCTGAGAAACCGC-1
AAACCTGAGAAACCTA-1
AAACCTGAGAAACGAG-1
AAACCTGAGAAACGCC-1
...
TTTGTCATCTTTACAC-2
TTTGTCATCTTTACGT-2
TTTGTCATCTTTAGGG-2
TTTGTCATCTTTAGTC-2
TTTGTCATCTTTCCTC-2

1474560 rows × 0 columns

barcodes = adata.obs_names
barcodes

Index(['AAACCTGAGAAACCAT-1', 'AAACCTGAGAAACCGC-1', 'AAACCTGAGAAACCTA-1',
       'AAACCTGAGAAACGAG-1', 'AAACCTGAGAAACGCC-1', 'AAACCTGAGAAAGTGG-1',
       'AAACCTGAGAACAACT-1', 'AAACCTGAGAACAATC-1', 'AAACCTGAGAACTCGG-1',
       'AAACCTGAGAACTGTA-1',
       ...
       'TTTGTCATCTTGGGTA-2', 'TTTGTCATCTTGTACT-2', 'TTTGTCATCTTGTATC-2',
       'TTTGTCATCTTGTCAT-2', 'TTTGTCATCTTGTTTG-2', 'TTTGTCATCTTTACAC-2',
       'TTTGTCATCTTTACGT-2', 'TTTGTCATCTTTAGGG-2', 'TTTGTCATCTTTAGTC-2',
       'TTTGTCATCTTTCCTC-2'],
      dtype='object', length=1474560)

gene_names = adata.var.index
print(gene_names)

Index(['DDX11L1', 'WASH7P', 'MIR6859-2', 'MIR1302-10', 'MIR1302-11', 'FAM138A',
       'OR4G4P', 'OR4G11P', 'OR4F5', 'RP11-34P13.7',
       ...
       'Tcrlibrary_RUNX1_1_gene', 'Tcrlibrary_RUNX1_2_gene',
       'Tcrlibrary_RUNX1_3_gene', 'Tcrlibrary_RUNX2_1_gene',
       'Tcrlibrary_RUNX2_2_gene', 'Tcrlibrary_RUNX2_3_gene',
       'Tcrlibrary_ZAP70_1_gene', 'Tcrlibrary_ZAP70_2_gene',
       'Tcrlibrary_ZAP70_3_gene', 'Cas9_blast_gene'],
      dtype='object', length=64370)

len(set(df_labels.barcode.tolist()))

1735

len(set(barcodes.tolist()))

1474560

matched_barcodes = sorted(set(barcodes.tolist()) & set(df_labels.barcode.tolist()))
len(matched_barcodes)

1735

# This is the InPathsY data in the original code of KPNNs
df_labels
barcode TCR
0 AAACCTGCACACATGT-1 0
1 AAACCTGCACGTCTCT-1 0
2 AAACCTGTCAATACCG-1 0
3 AAACCTGTCGTGGTCG-1 0
4 AAACGGGTCTGAGTGT-1 0
... ... ...
1730 TTTCCTCGTCATGCCG-2 1
1731 TTTGCGCGTAGCCTCG-2 1
1732 TTTGGTTAGATACACA-2 1
1733 TTTGGTTGTATGAATG-2 1
1734 TTTGGTTTCCAAGTAC-2 1

1735 rows × 2 columns

Import PKN with CORNETO#

cn.info()
Installed version:v1.0.0.dev43+3455818f
Available backends:CVXPY v1.6.6
Default backend (corneto.opt):CVXPY
Installed solvers:CLARABEL, HIGHS, OSQP, SCIPY, SCS
Graphviz version:v0.21
Installed path:/Users/pablorodriguezmier/Documents/work/repos/pablormier/corneto/corneto
Repository:https://github.com/saezlab/corneto
 
outputs_pkn = list(set(df_edges.parent.tolist()) - set(df_edges.child.tolist()))
inputs_pkn = set(df_edges.child.tolist()) - set(df_edges.parent.tolist())
input_pkn_genes = list(set(g.split("_")[0] for g in inputs_pkn))
len(inputs_pkn), len(outputs_pkn)

(13121, 1)

tuples = [(r.child, 1, r.parent) for _, r in df_edges.iterrows()]
G = cn.Graph.from_sif_tuples(tuples)
G = G.prune(inputs_pkn, outputs_pkn)

# Size of the original PKN provided by the authors
G.shape

(13439, 27579)

Select the single cell data for training#

adata_matched = adata[adata.obs_names.isin(matched_barcodes), adata.var_names.isin(input_pkn_genes)]
adata_matched.shape

(1735, 14229)

non_zero_genes = set(adata_matched.to_df().columns[adata_matched.to_df().sum(axis=0) >= 1e-6].values)
len(non_zero_genes)

12459

len(non_zero_genes.intersection(adata_matched.var_names))

12459

adata_matched = adata_matched[:, adata_matched.var_names.isin(non_zero_genes)]
# Many duplicates still 0 counts
adata_matched = adata_matched[:, adata_matched.to_df().sum(axis=0) != 0]
adata_matched.shape

(1735, 12487)

df_expr = adata_matched.to_df()
df_expr = df_expr.groupby(df_expr.columns, axis=1).max()
df_expr
A1BG A2ML1 AAAS AACS AADAT AAED1 AAGAB AAK1 AAMDC AAMP ... ZSWIM8 ZUFSP ZW10 ZWILCH ZXDC ZYG11A ZYG11B ZYX ZZEF1 ZZZ3
AAACCTGCACACATGT-1 0.0 0.0 0.000000 0.693147 0.0 0.000000 0.000000 0.000000 0.0 1.098612 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.000000
AAACCTGCACGTCTCT-1 0.0 0.0 0.000000 0.000000 0.0 0.693147 0.000000 0.000000 0.0 0.693147 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.000000
AAACCTGTCAATACCG-1 0.0 0.0 0.000000 0.000000 0.0 0.000000 0.000000 0.000000 0.0 0.693147 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.000000
AAACCTGTCGTGGTCG-1 0.0 0.0 1.098612 0.000000 0.0 0.000000 0.000000 0.000000 0.0 1.098612 ... 0.000000 0.693147 0.000000 0.693147 0.0 0.0 0.0 0.000000 0.000000 0.000000
AAACGGGTCTGAGTGT-1 0.0 0.0 0.000000 0.000000 0.0 0.693147 0.000000 0.000000 0.0 0.000000 ... 0.693147 0.000000 0.693147 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.000000
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
TTTCCTCGTCATGCCG-2 0.0 0.0 0.000000 0.000000 0.0 0.000000 0.000000 0.693147 0.0 0.693147 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.000000
TTTGCGCGTAGCCTCG-2 0.0 0.0 1.098612 0.000000 0.0 0.000000 0.000000 0.000000 0.0 1.386294 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.000000
TTTGGTTAGATACACA-2 0.0 0.0 1.098612 0.000000 0.0 0.000000 0.000000 1.098612 0.0 0.693147 ... 0.693147 0.000000 0.693147 0.000000 0.0 0.0 0.0 0.693147 0.693147 0.000000
TTTGGTTGTATGAATG-2 0.0 0.0 0.000000 0.000000 0.0 0.693147 1.098612 0.000000 0.0 0.693147 ... 0.000000 0.693147 0.000000 0.000000 0.0 0.0 0.0 0.000000 0.000000 0.693147
TTTGGTTTCCAAGTAC-2 0.0 0.0 0.000000 0.000000 0.0 0.000000 0.000000 0.000000 0.0 0.693147 ... 0.000000 0.000000 0.000000 0.000000 0.0 0.0 0.0 1.098612 0.000000 0.000000

1735 rows × 12459 columns

Building and training the KPNN#

Now we will use the provided PKN by the authors and the utility functions in CORNETO to build a KPNN similar to the one used in the original manuscript

import os

os.environ["KERAS_BACKEND"] = "jax"

import keras
from keras.callbacks import EarlyStopping
from sklearn.metrics import (
    accuracy_score,
    f1_score,
    precision_score,
    recall_score,
    roc_auc_score,
)
from sklearn.model_selection import StratifiedKFold

# Use the data from the experiment
X = df_expr.values
y = df_labels.set_index("barcode").loc[df_expr.index, "TCR"].values
X.shape, y.shape

((1735, 12459), (1735,))

# We can prefilter on top N genes to make this faster
top_n = None

# From the given PKN
outputs_pkn = list(set(df_edges.parent.tolist()) - set(df_edges.child.tolist()))
inputs_pkn = set(df_edges.child.tolist()) - set(df_edges.parent.tolist())
input_pkn_genes = list(set(g.split("_")[0] for g in inputs_pkn))

if top_n is not None and top_n > 0:
    input_pkn_genes = list(
        set(input_pkn_genes).intersection(df_expr.var(axis=0).sort_values(ascending=False).head(top_n).index)
    )
    inputs_pkn = list(g + "_gene" for g in input_pkn_genes)

len(inputs_pkn), len(outputs_pkn)

(13121, 1)

input_nn_genes = list(set(input_pkn_genes).intersection(df_expr.columns))
input_nn = [g + "_gene" for g in input_nn_genes]
len(input_nn)

12459

# Build corneto graph
tuples = [(r.child, 1, r.parent) for _, r in df_edges.iterrows()]
G = cn.Graph.from_sif_tuples(tuples)
G = G.prune(input_nn, outputs_pkn)
G.shape

(12767, 25928)

len(input_nn), len(input_nn_genes)

(12459, 12459)

len(set(input_nn).intersection(G.V))

12459

X = df_expr.loc[:, input_nn_genes].values
y = df_labels.set_index("barcode").loc[df_expr.index, "TCR"].values
X.shape, y.shape

((1735, 12459), (1735,))

from corneto._ml import build_dagnn


def stratified_kfold(
    G,
    inputs,
    outputs,
    n_splits=5,
    shuffle=True,
    random_state=42,
    lr=0.001,
    patience=10,
    file_weights="weights",
    dagnn_config=dict(
        batch_norm_input=True,
        batch_norm_center=False,
        batch_norm_scale=False,
        bias_reg_l1=1e-3,
        bias_reg_l2=1e-2,
        dropout=0.20,
        default_hidden_activation="sigmoid",
        default_output_activation="sigmoid",
        verbose=False,
    ),
):
    kfold = StratifiedKFold(n_splits=n_splits, shuffle=shuffle, random_state=random_state)
    models = []
    metrics = {m: [] for m in ["accuracy", "precision", "recall", "f1", "roc_auc"]}
    for i, (train_idx, val_idx) in enumerate(kfold.split(X, y)):
        X_train, X_val = X[train_idx], X[val_idx]
        y_train, y_val = y[train_idx], y[val_idx]

        print("Building DAG NN model with CORNETO using Keras with JAX...")
        print(f" > N. inputs: {len(input_nn)}")
        print(f" > N. outputs: {len(outputs_pkn)}")
        model = build_dagnn(G, input_nn, outputs_pkn, **dagnn_config)
        print(f" > N. parameters: {model.count_params()}")

        # Train the model with Adam
        opt = keras.optimizers.Adam(learning_rate=lr)
        early_stopping = EarlyStopping(monitor="val_loss", patience=patience, restore_best_weights=True)
        print("Compiling...")
        model.compile(optimizer=opt, loss="binary_crossentropy", metrics=["accuracy"])
        print("Fitting...")
        model.fit(
            X_train,
            y_train,
            validation_data=(X_val, y_val),
            epochs=200,
            batch_size=64,
            verbose=0,
            callbacks=[early_stopping],
        )

        if file_weights is not None:
            filename = f"{file_weights}_{i}.keras"
            model.save(filename)
            print(f"Weights saved to {filename}")

        # Predictions and metrics calculation
        y_pred_proba = model.predict(X_val).flatten()
        y_pred = (y_pred_proba > 0.5).astype(int)
        acc = accuracy_score(y_val, y_pred)
        precision = precision_score(y_val, y_pred)
        recall = recall_score(y_val, y_pred)
        f1 = f1_score(y_val, y_pred)
        roc_auc = roc_auc_score(y_val, y_pred_proba)
        metrics["accuracy"].append(acc)
        metrics["precision"].append(precision)
        metrics["recall"].append(recall)
        metrics["f1"].append(f1)
        metrics["roc_auc"].append(roc_auc)
        print(f" > Fold {i} validation ROC-AUC={roc_auc:.3f}")
        models.append(model)
    return models, metrics


temp_weights = tempfile.mkdtemp()
models, metrics = stratified_kfold(G, input_nn, outputs_pkn, file_weights=os.path.join(temp_weights, "weights"))

print("Validation metrics:")
for k, v in metrics.items():
    print(f" - {k}: {np.mean(v):.3f}")

Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 26236
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/weights_0.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 29s 3s/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 17s 2s/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 412ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 7s 412ms/step
 > Fold 0 validation ROC-AUC=0.991
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 26236
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/weights_1.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 16s 2s/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 12s 1s/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 308ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 5s 308ms/step
 > Fold 1 validation ROC-AUC=0.979
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 26236
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/weights_2.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 11s 1s/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 8s 942ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 123ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 208ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 208ms/step
 > Fold 2 validation ROC-AUC=0.982
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 26236
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/weights_3.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 11s 1s/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 7s 886ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 116ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 202ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 202ms/step
 > Fold 3 validation ROC-AUC=0.994
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 26236
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/weights_4.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 11s 1s/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 9s 1s/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 132ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 220ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 3s 220ms/step
 > Fold 4 validation ROC-AUC=0.992
Validation metrics:
 - accuracy: 0.964
 - precision: 0.969
 - recall: 0.958
 - f1: 0.963
 - roc_auc: 0.988

Now, we will analyze the learned biases for each of the nodes in the graph. Note that authors in the KPNN paper explain a way to extract weights for the nodes, based on the learned interactions and accounting for biases in the structure of the NN. Here we just show the learned biases of the nodes of the NN across 5 folds. Please be careful interpreting these weights.

# We collect the weights obtained in each fold


def load_biases(file="weights", folds=5):
    biases = []
    mean_inputs = []
    for i in range(5):
        model = keras.models.load_model(f"{file}_{i}.keras")
        for layer in model.layers:
            weights = layer.get_weights()
            if weights:
                biases.append((i, layer.name, weights[1][0]))
                mean_inputs.append((i, layer.name, weights[0].mean()))
    df_biases = pd.DataFrame(biases, columns=["fold", "gene", "bias"])
    df_biases["abs_bias"] = df_biases.bias.abs()
    df_biases["pow2_bias"] = df_biases.bias.pow(2)
    df_biases = df_biases.set_index(["fold", "gene"])
    return df_biases


df_biases = load_biases(file=os.path.join(temp_weights, "weights"), folds=5)
df_biases.sort_values(by="abs_bias", ascending=False).head(10)
bias abs_bias pow2_bias
fold gene
3 SUZ12.EZH2 -2.768535 2.768535 7.664784
4 PRKCD -2.499154 2.499154 6.245770
1 ZAP70 -2.205527 2.205527 4.864350
3 DUSP3 -2.144189 2.144189 4.597546
TCR -2.033000 2.033000 4.133087
4 LCK -2.014710 2.014710 4.059057
TCR 1.960717 1.960717 3.844413
3 PRKCD -1.850238 1.850238 3.423379
0 TCR -1.836677 1.836677 3.373384
PRKCD 1.777246 1.777246 3.158603 
df_biases_full = df_biases.copy().reset_index()
gene_biases_score = df_biases_full.groupby("gene")["pow2_bias"].mean().sort_values(ascending=False)
gene_biases_score

gene
TCR             3.427786
PRKCD           3.129591
SUZ12.EZH2      2.498496
LCK             1.725973
p38             1.404157
                  ...   
MLL2.complex    0.000493
HMT             0.000109
HSF2            0.000087
GATA3           0.000080
REST            0.000022
Name: pow2_bias, Length: 308, dtype: float32

gene_biases_score.head(30).plot.bar()

<Axes: xlabel='gene'>
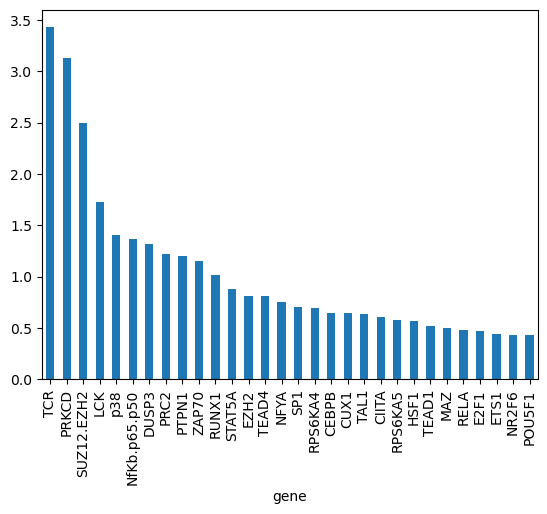
../../_images/bdce21ef392c9bc0e719fafa057daf02435bcf07217c2bc5eb525c31f15d19ce.png 
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

# Get the top genes sorted by mean bias
top_genes = gene_biases_score.head(30).index

# Filter the DataFrame to include only rows with these top genes
filtered_df = df_biases_full[df_biases_full["gene"].isin(top_genes)]

plt.figure(figsize=(10, 6))
sns.violinplot(data=filtered_df, x="gene", y="bias", order=top_genes, dodge=True)
sns.stripplot(data=filtered_df, x="gene", y="bias", order=top_genes, dodge=True)
plt.xticks(rotation=90)
plt.title("Biases of the trained neurons")
plt.xlabel("Gene")
plt.ylabel("Bias")
plt.axhline(0, linestyle="--", color="k")
plt.tight_layout()
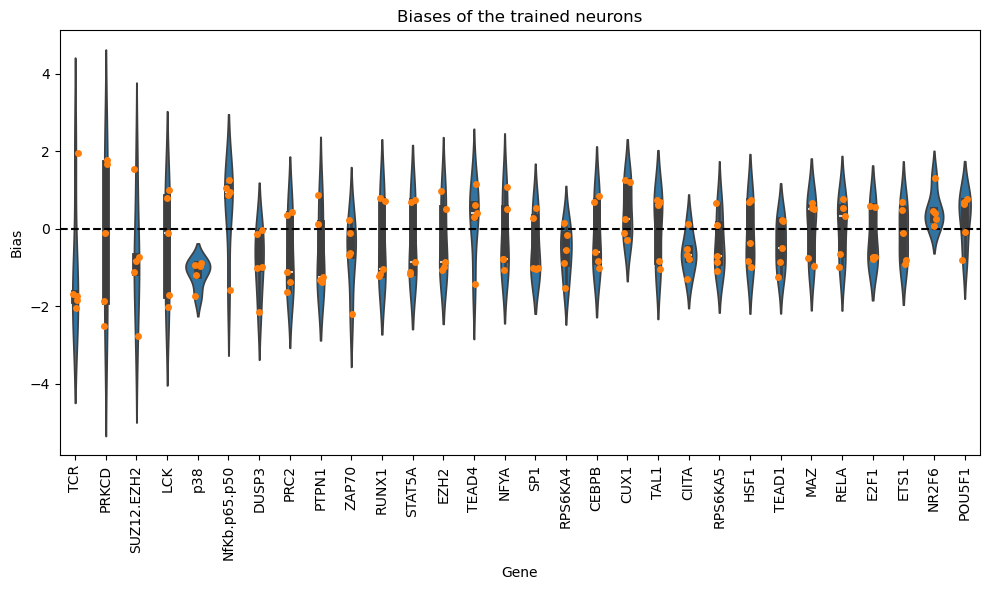
../../_images/3eb465cddf5a80bcb80c6135bc1db8b1a9183ca2ae42ea6f174483428f63ca0f.png

Use CORNETO for NN pruning#

Now we will show how CORNETO can be used to extract a smaller, yet complete DAG from the original PKN provided by the authors. We will add input edges to each input node and an output edge through TCR to indicate which nodes are the inputs and which one the output. We will use then Acyclic Flow to find the smallest DAG comprising these nodes

G_dag = G.copy()
new_edges = []
for g in input_nn:
    new_edges.append(G_dag.add_edge((), g))
new_edges.append(G_dag.add_edge("TCR", ()))
print(G_dag.shape)

# Find small DAG. We use Acyclic Flow to find over the space of DAGs
P = cn.opt.AcyclicFlow(G_dag)
# We enforce that the input genes and the output gene are part of the solution
P += P.expr.with_flow[new_edges] == 1
# Minimize the number of active edges
P.add_objectives(sum(P.expr.with_flow), weights=1)
P.solve(solver="SCIP", verbosity=1, max_seconds=300);

(12767, 38388)
===============================================================================
                                     CVXPY                                     
                                     v1.6.6                                    
===============================================================================
-------------------------------------------------------------------------------
                                  Compilation                                  
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
                                Numerical solver                               
-------------------------------------------------------------------------------
Running HiGHS 1.8.0 (git hash: 222cce7): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e-04, 1e+04]
  Cost   [1e+00, 1e+00]
  Bound  [1e+00, 1e+00]
  RHS    [1e+00, 1e+04]
Presolving model
83375 rows, 57447 cols, 205995 nonzeros  0s
40079 rows, 41245 cols, 128297 nonzeros  0s
39352 rows, 38165 cols, 131120 nonzeros  0s
Objective function is integral with scale 1

Solving MIP model with:
   39352 rows
   38165 cols (18825 binary, 0 integer, 0 implied int., 19340 continuous)
   131120 nonzeros
MIP-Timing:        0.54 - starting analytic centre calculation

Src: B => Branching; C => Central rounding; F => Feasibility pump; H => Heuristic; L => Sub-MIP;
     P => Empty MIP; R => Randomized rounding; S => Solve LP; T => Evaluate node; U => Unbounded;
     z => Trivial zero; l => Trivial lower; u => Trivial upper; p => Trivial point

        Nodes      |    B&B Tree     |            Objective Bounds              |  Dynamic Constraints |       Work      
Src  Proc. InQueue |  Leaves   Expl. | BestBound       BestSol              Gap |   Cuts   InLp Confl. | LpIters     Time

         0       0         0   0.00%   19693           inf                  inf        0      0      0         0     0.5s
         0       0         0   0.00%   19693           inf                  inf        0      0      1     19806     1.8s
         0       0         0   0.00%   22669.402362    inf                  inf     5152   3535    132     39839     7.3s
 L       0       0         0   0.00%   22669.405102    25088              9.64%     5152   3535    258     39839    19.3s

0.2% inactive integer columns, restarting
Model after restart has 39282 rows, 38128 cols (18793 bin., 0 int., 0 impl., 19335 cont.), and 130976 nonzeros

         0       0         0   0.00%   22669.405102    25088              9.64%     3297      0      0     92375    19.6s
         0       0         0   0.00%   22669.405102    25088              9.64%     3297   3175      4    136853    33.4s
         0       0         0   0.00%   22995.391228    25088              8.34%     4679   3772      4    146501    38.4s

Symmetry detection completed in 3.9s
Found 2264 generator(s)
        55       0         1   0.00%   22996.391797    25088              8.34%     6285   3695    172    303808   149.4s
       220     217         2   0.00%   23067.071606    25088              8.06%     6286   3695    481    316586   205.1s
       250     216         3   0.00%   23067.071606    25088              8.06%     6394   3737    528    407997   278.4s
       280     274         4   0.00%   23067.071606    25088              8.06%     6395   3737    613    413452   300.0s
       280     274         4   0.00%   23067.071606    25088              8.06%     6395   3737    613    413452   300.0s

Solving report
  Status            Time limit reached
  Primal bound      25088
  Dual bound        23068
  Gap               8.05% (tolerance: 0.01%)
  P-D integral      23.3781609893
  Solution status   feasible
                    25088 (objective)
                    0 (bound viol.)
                    0 (int. viol.)
                    0 (row viol.)
  Timing            300.04 (total)
                    0.00 (presolve)
                    0.00 (solve)
                    0.00 (postsolve)
  Max sub-MIP depth 8
  Nodes             280
  Repair LPs        0 (0 feasible; 0 iterations)
  LP iterations     413452 (total)
                    176391 (strong br.)
                    35258 (separation)
                    52536 (heuristics)
Solver terminated with message: Time limit reached. (HiGHS Status 13: Time limit reached)
-------------------------------------------------------------------------------
                                    Summary                                    
-------------------------------------------------------------------------------

G_subdag = G_dag.edge_subgraph(P.expr.with_flow.value > 0.5)
G_dag.shape, G_subdag.shape

((12767, 38388), (12629, 25088))

rel_dag_compression = (1 - (G_subdag.num_edges / G_dag.num_edges)) * 100
print(f"KPNN edge compression (0-100%): {rel_dag_compression:.2f}%")

KPNN edge compression (0-100%): 34.65%

pruned_models, pruned_metrics = stratified_kfold(
    G_subdag,
    input_nn,
    outputs_pkn,
    file_weights=os.path.join(temp_weights, "pruned_weights"),
)

print("Validation metrics:")
for k, v in pruned_metrics.items():
    print(f" - {k}: {np.mean(v):.3f}")

Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 12798
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/pruned_weights_0.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 5s 583ms/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 4s 517ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 111ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 111ms/step
 > Fold 0 validation ROC-AUC=0.994
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 12798
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/pruned_weights_1.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 6s 666ms/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 4s 476ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 64ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 108ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 108ms/step
 > Fold 1 validation ROC-AUC=0.977
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 12798
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/pruned_weights_2.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 6s 649ms/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 5s 556ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 72ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 121ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 121ms/step
 > Fold 2 validation ROC-AUC=0.986
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 12798
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/pruned_weights_3.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 6s 622ms/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 4s 480ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 106ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 106ms/step
 > Fold 3 validation ROC-AUC=0.995
Building DAG NN model with CORNETO using Keras with JAX...
 > N. inputs: 12459
 > N. outputs: 1
 > N. parameters: 12798
Compiling...
Fitting...
Weights saved to /var/folders/b4/gwkwsdb93sv11rtztqbm3l040000gn/T/tmp044vf9e8/pruned_weights_4.keras

 1/11 ━━━━━━━━━━━━━━━━━━━━ 5s 566ms/step

 2/11 ━━━━━━━━━━━━━━━━━━━━ 4s 489ms/step

10/11 ━━━━━━━━━━━━━━━━━━━━ 0s 64ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 0s 107ms/step

11/11 ━━━━━━━━━━━━━━━━━━━━ 2s 107ms/step
 > Fold 4 validation ROC-AUC=0.995
Validation metrics:
 - accuracy: 0.964
 - precision: 0.969
 - recall: 0.958
 - f1: 0.963
 - roc_auc: 0.989

df_biases_pruned = load_biases(file=os.path.join(temp_weights, "pruned_weights"), folds=5)
df_biases_pruned.sort_values(by="abs_bias", ascending=False).head(10)
bias abs_bias pow2_bias
fold gene
4 RUNX1 -2.475160 2.475160 6.126415
SUZ12.EZH2 -2.461908 2.461908 6.060989
2 SUZ12.EZH2 -2.451049 2.451049 6.007642
1 SUZ12.EZH2 -2.388376 2.388376 5.704338
3 PRKCD -2.239764 2.239764 5.016545
RUNX1 2.021947 2.021947 4.088270
PRC2 -1.983842 1.983842 3.935630
4 TAL1 -1.962536 1.962536 3.851547
0 ZAP70 1.947543 1.947543 3.792922
TCR 1.871278 1.871278 3.501682 
df_biases_prunedr = df_biases_pruned.copy().reset_index()
gene_biases_score = df_biases_prunedr.groupby("gene")["pow2_bias"].mean().sort_values(ascending=False)
gene_biases_score

gene
SUZ12.EZH2    3.994649e+00
RUNX1         3.776556e+00
TAL1          2.716972e+00
ETS1          2.500564e+00
TCR           2.426713e+00
                  ...     
KMT2D         5.081624e-03
TBP           1.791134e-03
HMT           4.137235e-04
ASH2L         3.378770e-06
GATA3         7.418886e-09
Name: pow2_bias, Length: 170, dtype: float32

gene_biases_score.head(30).plot.bar()

<Axes: xlabel='gene'>
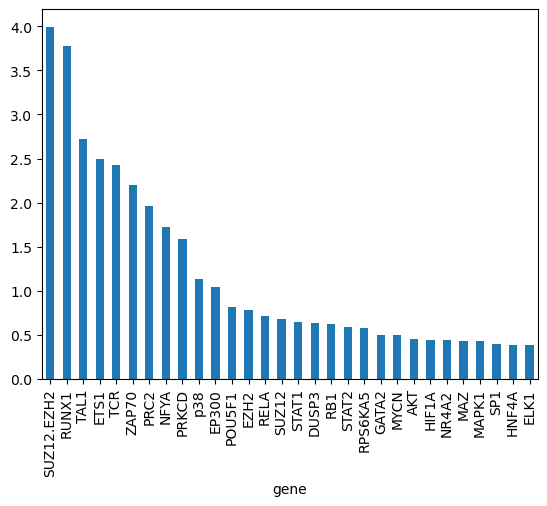
../../_images/1beffdb8b52a19c21260449f0df1c97916b85bae018c6b56b1769d682c6208ed.png 
# Get the top genes sorted by mean bias
top_genes = gene_biases_score.head(30).index

# Filter the DataFrame to include only rows with these top genes
filtered_df = df_biases_prunedr[df_biases_prunedr["gene"].isin(top_genes)]

plt.figure(figsize=(10, 6))
sns.violinplot(data=filtered_df, x="gene", y="bias", order=top_genes, dodge=True)
sns.stripplot(data=filtered_df, x="gene", y="bias", order=top_genes, dodge=True)
plt.xticks(rotation=90)
plt.title("Biases of the trained neurons")
plt.xlabel("Gene")
plt.ylabel("Bias")
plt.axhline(0, linestyle="--", color="k")
plt.tight_layout()
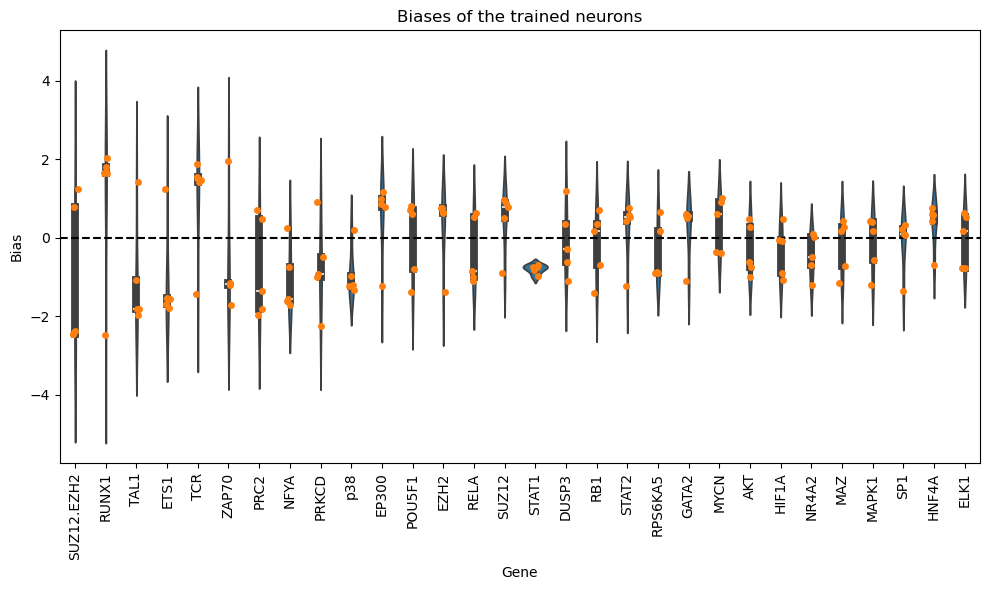
../../_images/34b400d1e5cf9fa95375471210314966d0c92d32d39e551f536360828314c2ef.png 
param_compression = (1 - (pruned_models[0].count_params() / models[0].count_params())) * 100
print(f"Parameter compression: {param_compression:.2f}%")

Parameter compression: 51.22%

perf_degradation = (
    (np.mean(metrics["roc_auc"]) - np.mean(pruned_metrics["roc_auc"])) / np.mean(metrics["roc_auc"])
) * 100
print(
    f"Degradation in ROC-AUC after compression (positive = decrease in performance, negative = increase in performance): {perf_degradation:.2f}%"
)

Degradation in ROC-AUC after compression (positive = decrease in performance, negative = increase in performance): -0.19%